Featured Resources:
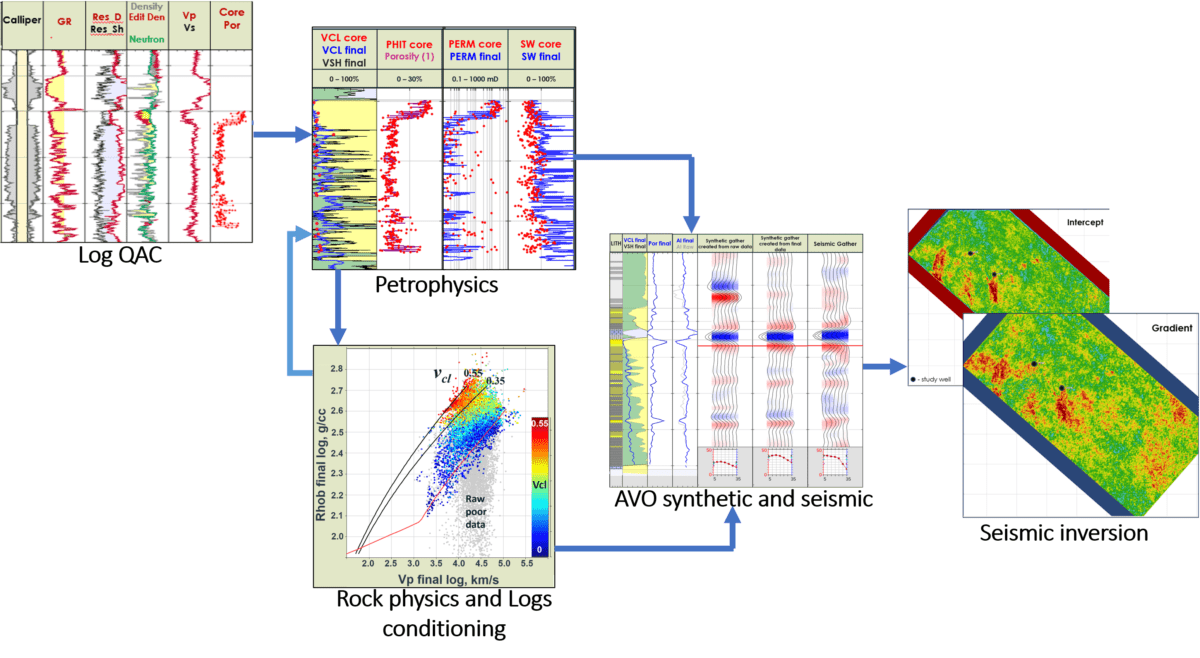
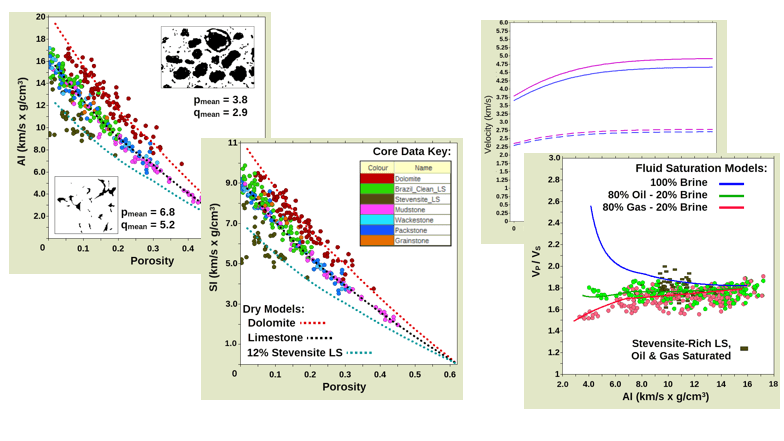
Video: Well Log QAC and Rock Physics Modelling in a Data-poor Environment
Topic
Locations
By submitting this form, you are consenting to receive marketing emails from: Ikon Science, 1 The Crescent, Surbiton, Greater London, KT6 4BN United Kingdom, https://www.ikonscience.com/. You can revoke your consent to receive emails at any time by using the SafeUnsubscribe SafeUnsubscribe® link, found at the bottom of every email.