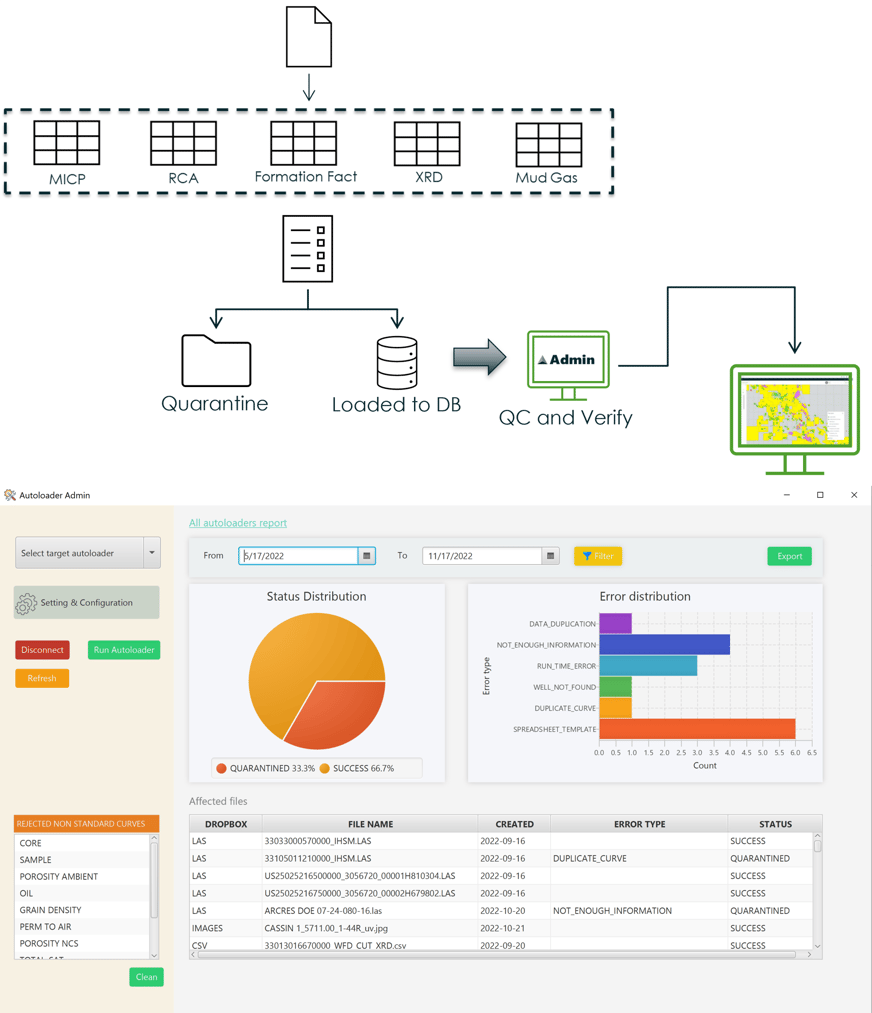
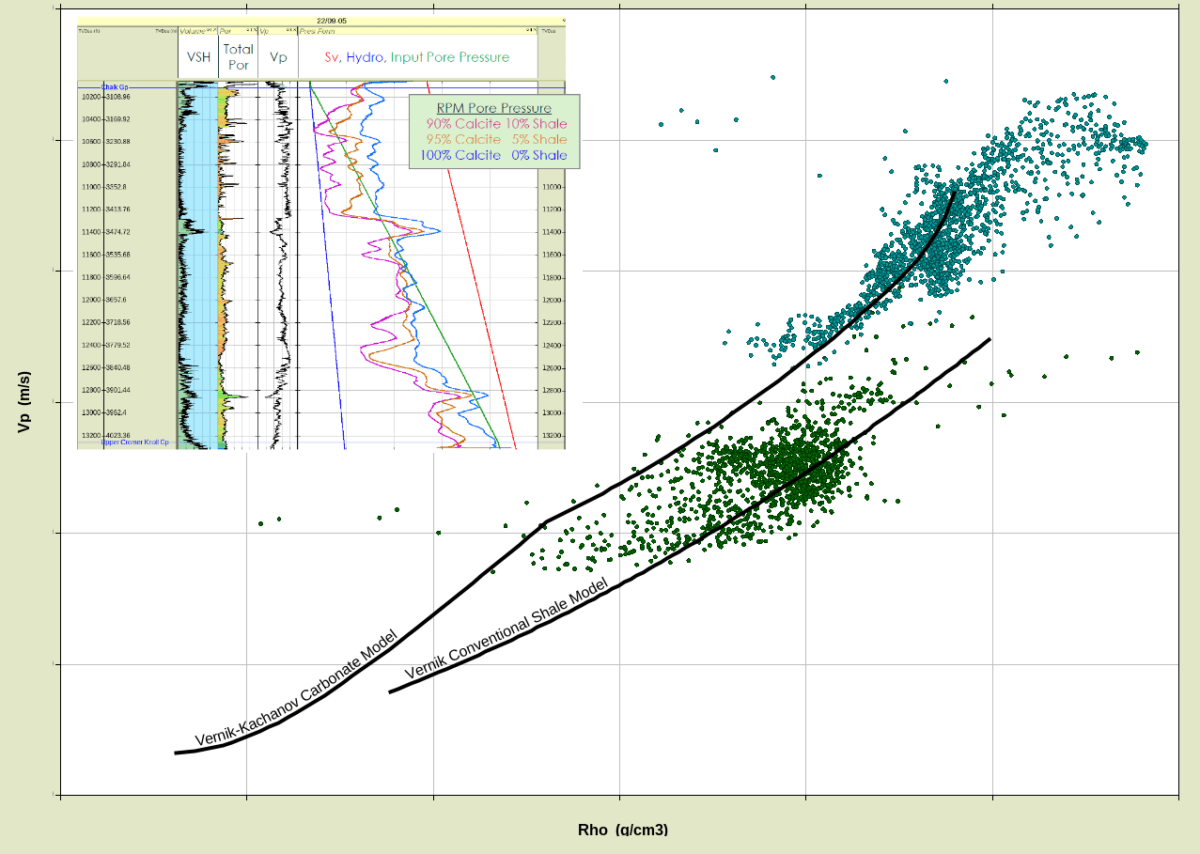
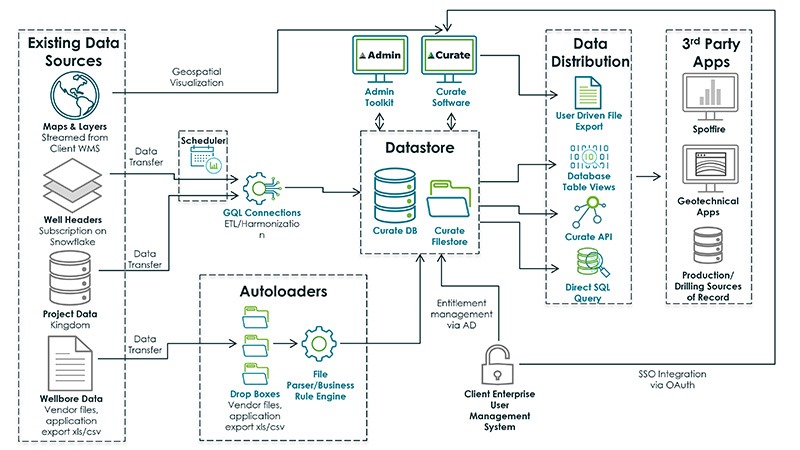
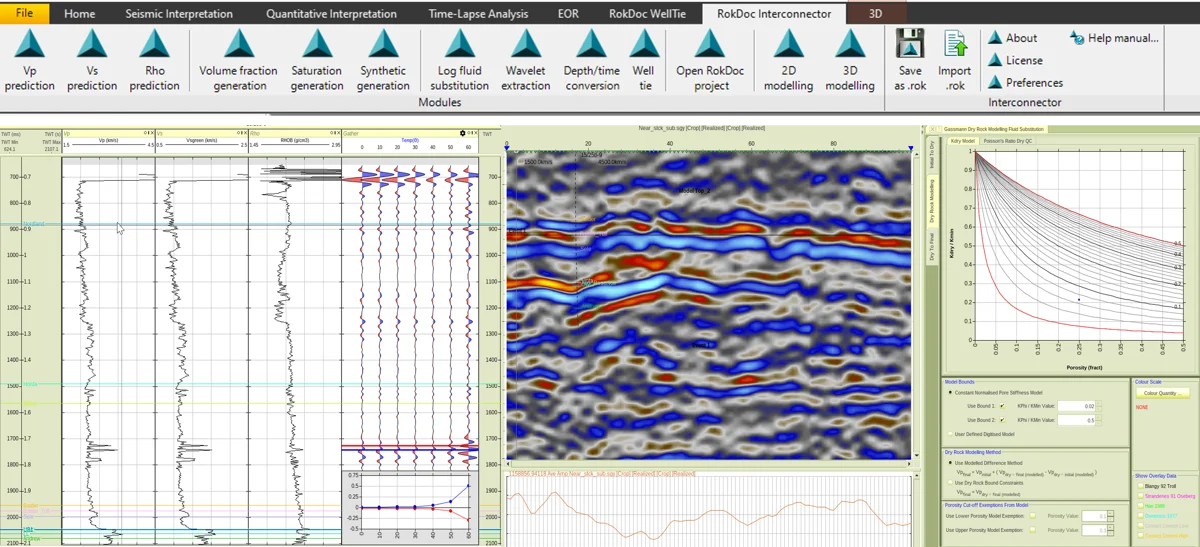
Featured Resources:
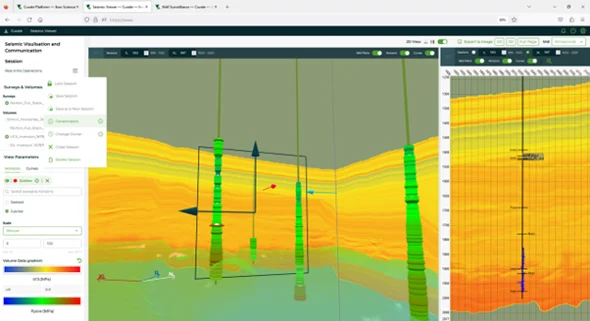
Webinars: Great Data Isn’t Enough; It Has to Be Usable – Curate 2025.2
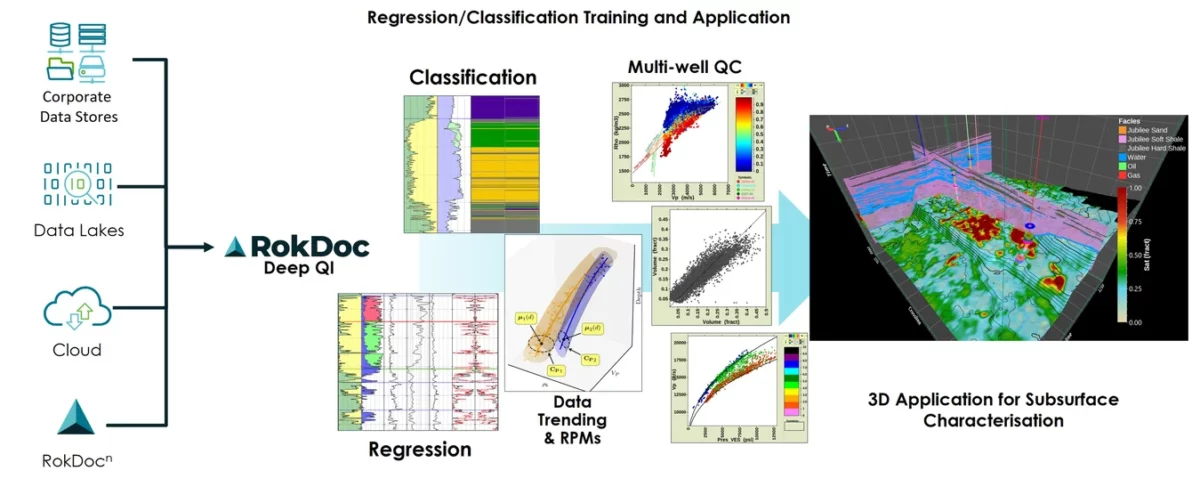
Webinars: Smarter Subsurface Workflows, Faster Insights: Unveiling RokDoc 2025.2
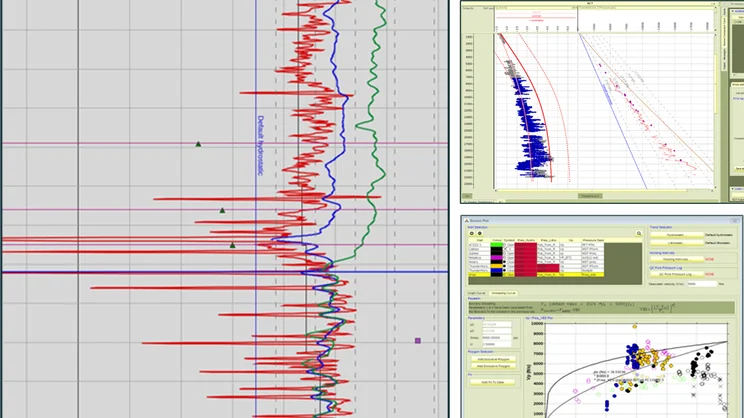
Video: Exploratory Data Analysis (EDA) Tool for Well-Log Data
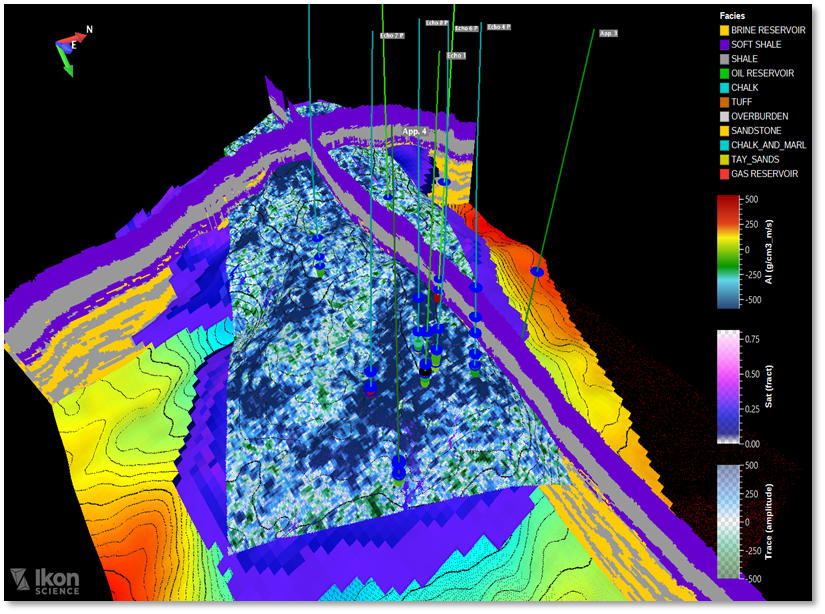
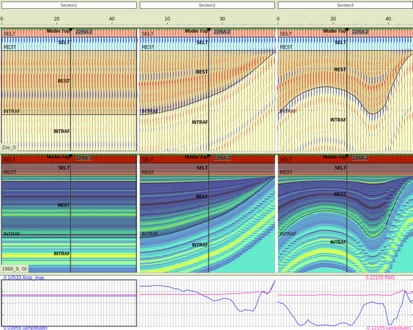
Video: Enhancing Reservoir Management a Comprehensive 4D Monitoring Approach Through Rock Physics